Introduction
On this page I'll mathematically derive some results for circles colliding and use the results for a simple physics engine implemented in C++ with SFML!
Theory
Suppose we have a large stationary circle of radius \(R\) and a smaller, moving circle of radius \(r\) which accelerates freely under gravity, without air resistance. Suppose also that the larger circle is lodged into place, so that, even after colliding with the smaller circle, the larger circle does not move. The smaller circle is dropped straight down, so it has no horizontal velocity. Assume that the collision is elastic (i.e. no energy is lost). This seems like a lot of assumptions, but when making a model like this it tends to be easier to start simple before complicating, because simple models can be quite accurate.
For our physics engine, we want to know what the final velocity of the smaller circle will be after the collision, in terms of known parameters. Take a look at this diagram below, which illustrates the geometry at the point of collision:
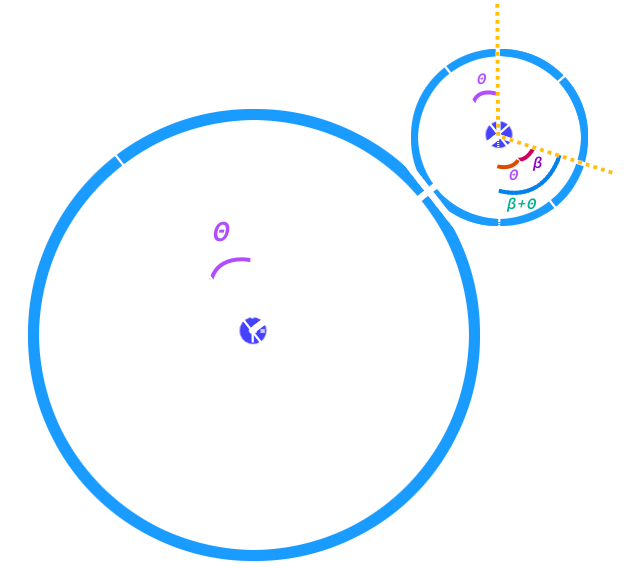
The tangent line (the thick white line squashed between the 2 circles) acts as the surface which the smaller circle "bounces off" of. That is to say, the smaller circle colliding with the large circle at that point is equivalent to the smaller circle colliding with the tangent line at the same point. This tangent line is useful for the geometry of the problem.
We set \(\theta\) to be the angle (the argument) between the two circle centers (measured from the horizontal at the large circle to the smaller circle) and this quantity can be calculated easily in code. We let \(v\) be the speed of the smaller circle, which is known inside the engine. Since energy is conserved (by assumption -- it's an elastic collision) the velocity immediately after the collision must be \(v\) also.
The change of direction of the smaller circle occurs by an impulse from the larger circle (due to the normal contact force) and this impulse is directed perpendicular to the surface of collision. Since the impulse is perpendicular, no work is done parallel to the surface, so the velocity parallel to the plane before and after are the same, in other words, \(v\cos\theta = v\cos\beta\), and so \(\theta = \beta\).
The angle marked in blue is therefore \(2\theta\), and this is very important, because this gives us a way of representing the final velocity in terms of its \(x\)-\(y\) components. Using trigonometry we see that $$\vec{v_F} = v\cdot\begin{pmatrix}\sin{2\theta}\\\cos{2\theta}\end{pmatrix}$$ which basically concludes what calculation we need to do at collision point.
Equation of motion
On earth, objects are affected by the gravitational pull towards the center of the & accelerate at a rate which is practically uniform at \(9.81\text{ms}^{-2}\). As a matter of fact, the acceleration isn't uniform, but it is always around this value near the surface of the earth, so we make the well-justified assumption (paired with the absense of air resistance) that all objects accelerate at this constant value. If the acceleration is constant, the position must be a quadratic function, which we can see by calculus:$$v(t) = \int \frac{\mathrm{d}v}{\mathrm{d}t} \mathrm{d}t = \int a \hspace{.5em}\mathrm{d}t = at + C$$ $$s(t) = \int v\hspace{.5em}\mathrm{d}t = \int at + C \hspace{.5em} = \frac{a}{2}t^2 + Ct + D$$ (Note that \(C\) and \(D\) are the initial velocity & initial position respectively; Im gona continue this tomorrow if anyonesreading it becomes more interesting and philosphical trust me)