Introduction
This series of pages proves the mean value theorem without requiring any prior knowledge. We start from the construction of the real numbers and build from there. Many people have become confused due to a lack of holistic understanding of the concepts involved in proving the statement.
This page introduces the theorem and how it is used. If you can't understand some terminology on this page, then do not worry - the terms will be explained as we go
Theorem statement
The theorem states that if \(f\) is a continuous function on the closed interval \([a,b]\) and is differentiable on the open interval \((a,b)\), then there exists a real number \(c\) in \((a,b)\) such that the following equation holds: \[f'(c) = \frac{f(b)-f(a)}{b-a}\] The terminology rendered in italics will be defined in the subsequent pages.
Graphical interpretation
If you draw a smooth curve on the \(x\)-\(y\) plane between two points, and the curve does not go "back in" on itself (i.e. there is only a single \(y\) value for a given \(x\) value), then it will be possible to draw a tangent line parallel to the secant line connecting the two points.
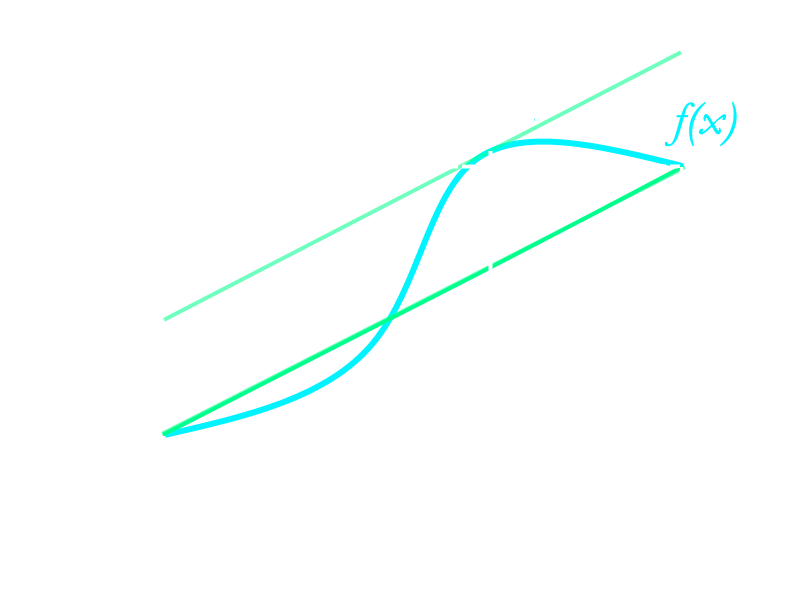
The two points in question here are \((a, f(a)\)) and \((b, f(b))\). By the mean value theorem, we can draw a line which touches the curve (a tangent line) at some point \((c, f(c))\) on the curve, with the property that this line is parallel to the line connecting \((a, f(a))\) and \((b, f(b))\) (the secant line).
In the figure above, the secant line is shown in an opaque teal while the tangent lines given by the mean value theorem is shown as transparent.
Notice how there is another value \(c\) of which gives a tangent line (shown below) parallel to the secant line. The mean value theorem doesn't indicate how many values of \(c\) satisfy \(f'(c)=\frac{f(b)-f(a)}{b-a}\); in fact, the MVT does not even tell you the actual value(s) of \(c\) -- it only states that such a value exists. This type of theorem is called an existence theorem.
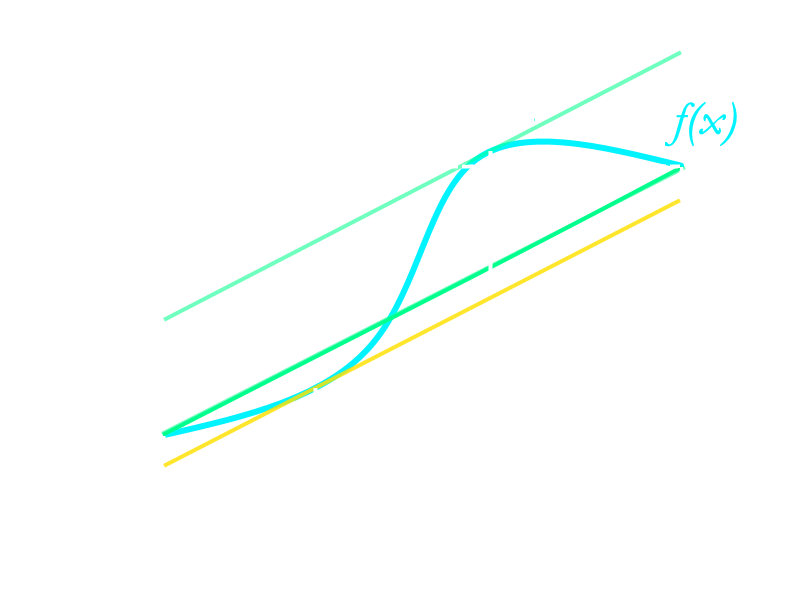
(Both of the values of \(c\) on \((a,b)\) satisfying \(f'(c) = \frac{f(b)-f(a)}{b-a}\) are shown on this diagram)
Another example of an existence theorem is the extreme value theorem which states that, if a function is continuous on an interval, then the function in question attains a maximum value (and also a minimum value) somewhere in that interval. This theorem is used in proving the MVT.
Consequences
The mean value theorem is used in order to prove:
- most importantly: the fundamental theorem of calculus (since said theorem follows from the MVT, the MVT is more fundamental)
- Taylor's theorem (that a non-polynomial function can be expressed as an infinite polynomial)
- L'Hospital's rule (a theorem used to find certain limits)
- that a function is strictly increasing if its derivative is positive
- that a function with a zero derivative in an interval is constant in said interval